논리회로
지난번 글에서 컴퓨터는 2진수를 통해 데이터를 인식한다고 설명했습니다. 트랜지스터는 전류가 흐르거나 흐르지 않는 상태를 통해 1 또는 0으로 나타낼 수 있습니다. 즉, 트랜지스터를 통해 컴퓨터가 인식할 수 있는 데이터를 나타낼 수 있습니다.
논리회로(Logic Gate)
트랜지스터를 도식화하면 다음과 같은데, Gate에 전압을 걸어주거나 걸어주지 않는 것으로 Drain으로 전류를 흐르게 하거나 흐르지 않게 할 수 있습니다.
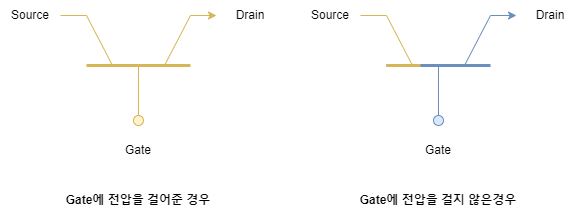
이런 트랜지스터의 특성을 통해 스위치 역할을 함으로써 논리회로(Logic Gate)를 만들 수 있습니다.
NOT gate
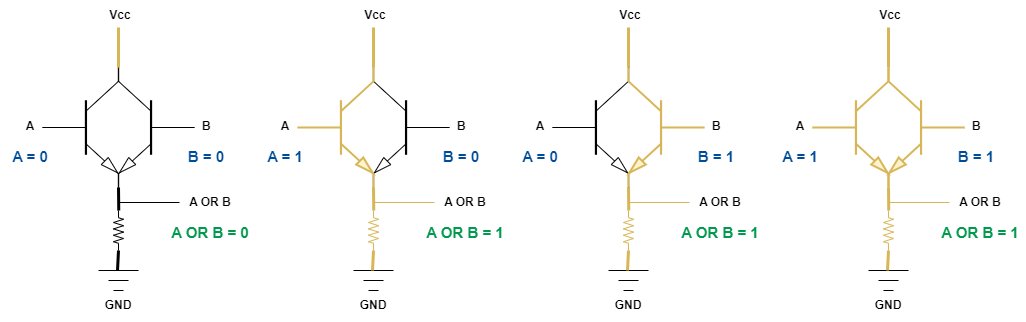
NOT gate는 참을 거짓으로, 거짓을 참으로 출력하는 회로입니다. 즉, Gate에 전류가 흐르면 거짓, 전류가 흐르지 않으면 참을 출력합니다.
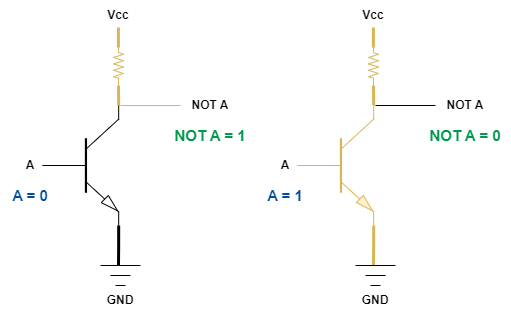
A에 전류가 흐르지 않으면 GND로 전류가 흐르지 않아서 출력선으로 전류가 흐르게 됩니다. 즉, 참을 출력합니다.
반면에 A에 전류가 흐르면 GND로 전류가 흐를 수 있어서 출력선으로는 전류가 흐르지 않습니다. 즉, 거짓을 출력합니다.
진리표
| A | NOT A |
|---|---|
| 1 | 0 |
| 0 | 1 |
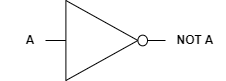
논리식은 $ \bar A $로 나타내며, 기호는 다음과 같습니다.
AND gate
AND gate는 두 입력선이 모두 참이면 참, 아니면 거짓을 출력하는 회로입니다.
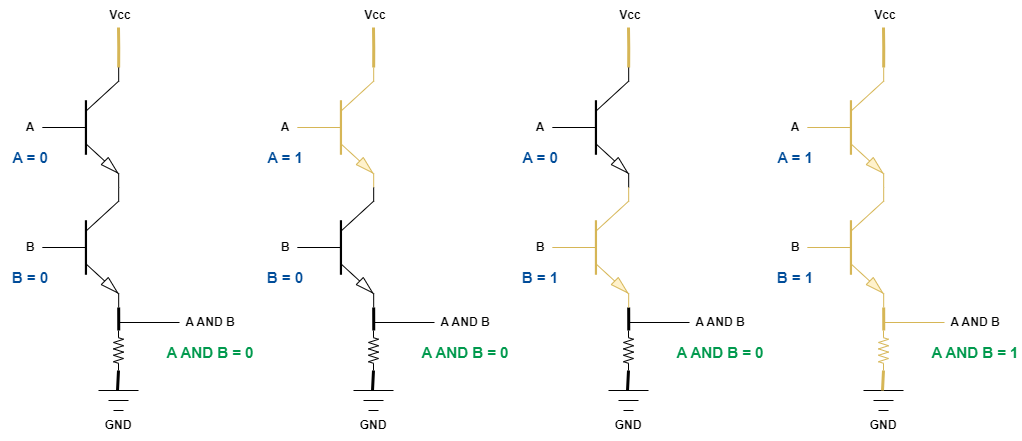
진리표
| A | B | A AND B |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
논리식은 $ A \cdot B $로 나타내며, 기호는 다음과 같습니다.
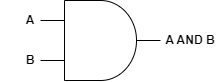
OR gate
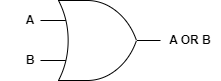
OR gate는 두 입력선 중 하나라도 참이면 참을 출력하는 회로입니다.
진리표
| A | B | A OR B |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
논리식은 $ A + B $로 나타내며, 기호는 다음과 같습니다.
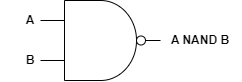
NAND gate
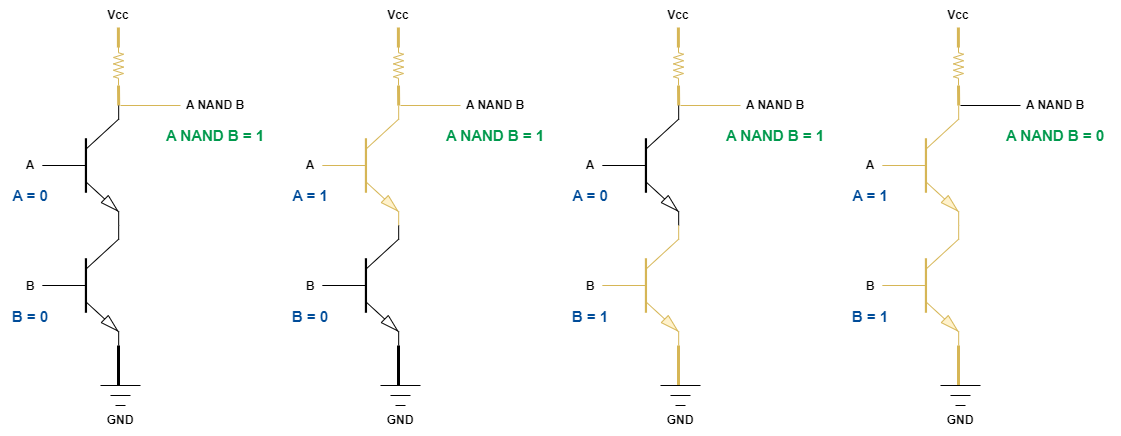
NAND gate는 AND gate의 반대값을 출력하는 회로입니다. 즉, 모든 입력이 참일 경우에만 거짓을 출력합니다.
진리표
| A | B | A NAND B |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
논리식은 $ \overline {A \cdot B} $로 나타내며, 기호는 다음과 같습니다.
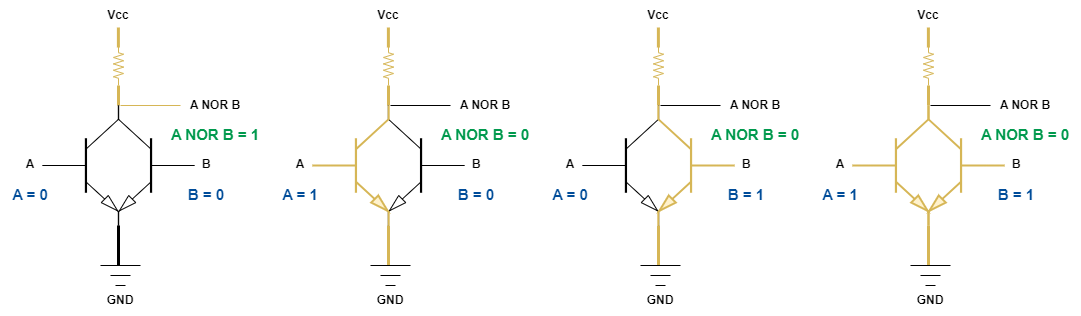
NOR gate
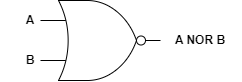
NOR gate는 OR gate의 반대값을 출력하는 회로입니다. 즉, 두 입력선 중 하나라도 참일 경우에는 거짓을 출력합니다.
진리표
| A | B | A NOR B |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 0 |
논리식은 $ \overline {A + B} $로 나타내며, 기호는 다음과 같습니다.
XOR gate
XOR gate는 배타적 논리합을 구현한 회로입니다. 즉, 두 입력선의 값이 서로 다른 경우에만 참을 출력합니다. 논리식은 $ A \oplus B $로 나타내며, $ \bar A \cdot B + A \cdot \bar B $와 같습니다.
진리표
| A | B | $ \bar A \cdot B $ | $ A \cdot \bar B $ | A XOR B |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 0 |
위 논리식을 토대로 회로를 구성하면 다음과 같습니다.
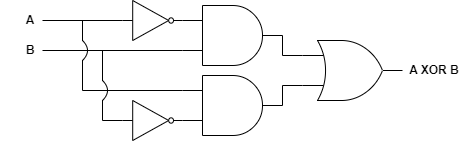
기호는 다음과 같습니다.
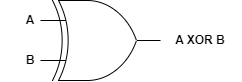
XNOR gate
XOR gate는 XOR gate의 반대값을 출력하는 회로입니다. 즉, 두 입력선의 값이 서로 같은 경우에만 참을 출력합니다. 논리식은 $ \overline {A \oplus B} $ 또는 $ A⊙B $로 나타내며, $ \bar A \cdot \bar B + A \cdot B $와 같습니다.
진리표
| A | B | $ \bar A \cdot \bar B $ | $ A \cdot B $ | A XNOR B |
|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 |
위 논리식을 토대로 회로를 구성하면 다음과 같습니다.
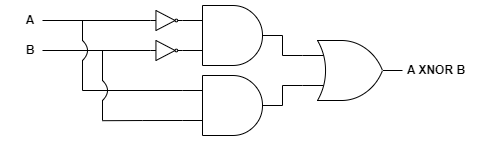
기호는 다음과 같습니다.
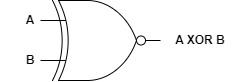
조합회로(Combinational Circuit)
조합회로는 출력값이 입력값에만 영향을 받는 논리회로입니다. 논리회로에 입력이 주어지면 바로 출력이 나오며, 이전의 회로 상태가 출력에 영향을 미치지 않습니다. 즉, 메모리 소자를 가지지 않습니다.
가산기(Adder)
가산기(Adder)는 입력들의 합을 출력하는 논리회로입니다. 가산기에는 2개의 입력을 더하는 반가산기(Half Adder, HA)와, 3개의 입력을 더하는 전가산기(Full Adder, FA)가 있습니다.
1. 반가산기(Half Adder, HA)
반가산기(HA)는 2진수 한 자리를 덧셈하여 캐리(Carry)와 덧셈의 결과를 출력합니다. 반가산기의 진리표는 아래와 같습니다.
| A | B | 캐리(C) | 덧셈(S) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
진리표를 보면, 올림수인 캐리는 AND gate, 덧셈의 결과는 XOR gate와 동일함을 알 수 있습니다. 회로는 다음과 같습니다.
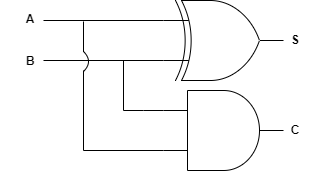
반가산기의 경우 캐리에 대한 입력을 받지 않기 때문에 최하위 비트(Least Significant Bit, LSB)에서만 사용할 수 있습니다.
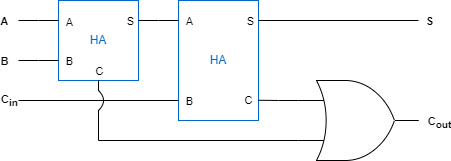
2. 전가산기(Full Adder, FA)
전가산기(FA)는 반가산기에 캐리를 추가한 3개의 입력을 더하여 캐리와 덧셈의 결과를 출력하는 회로입니다. 전가산기의 진리표는 아래와 같습니다.
| A | B | Cin | Cout | S |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
진리표만으로는 회로를 설계하기 어렵습니다. 논리식을 설계하기위해 카르노맵을 그려보겠습니다. 카르노맵에 대한 설명은 이 글에서 생략합니다.
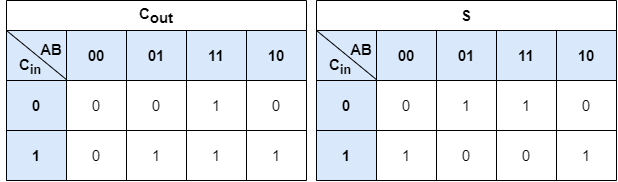
카르노맵을 통해 다음과 같은 논리식을 설계할 수 있습니다.
$$ \begin{aligned} C_{out} &= \bar A \cdot B \cdot C_{in} + A \cdot \bar B \cdot C_{in} + A \cdot B \cdot \bar C_{in} + A \cdot B \cdot C_{in} \\ &= (\bar A \cdot B + A \cdot \bar B) \cdot C_{in} + A \cdot B \cdot (\bar C_{in} + C_{in}) \\ &= (A \oplus B) \cdot C_{in} + A \cdot B \\ \\ S &= \bar A \cdot B \cdot \bar C_{in} + A \cdot \bar B \cdot \bar C_{in} + \bar A \cdot \bar B \cdot C_{in} + A \cdot B \cdot C_{in} \\ &= (\bar A \cdot B + A \cdot \bar B) \cdot \bar C_{in} + (\bar A \cdot \bar B + A \cdot B) \cdot C_{in} \\ &= A \oplus B \cdot \bar C_{in} + A \odot B \cdot C_{in} \\ &= A \oplus B \cdot \bar C_{in} + \overline{A \oplus B} \cdot C_{in} \\ &= A \oplus B \oplus C_{in} \end{aligned} $$
해당 논리식을 토대로 회로를 그리면 다음과 같습니다.
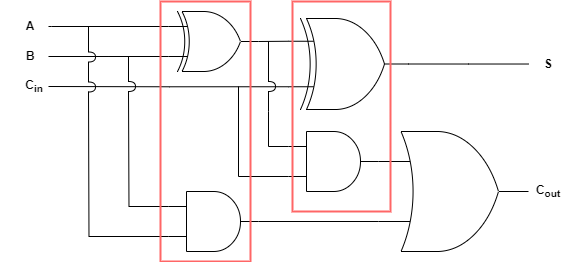
2개의 반가산기와 OR gate로 구성되어 있음을 알 수 있습니다. 간략화하면 다음과 같습니다.
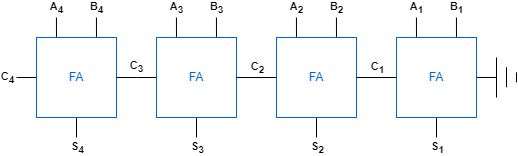
전가산기 n개를 병렬로 연결한다면 리플 캐리 가산기(Ripple Cary Adder)라는 n비트 가산기를 만들 수 있습니다.
가산기의 B 입력을 부호 플래그와 XOR하여 사용한다면 덧셈과 뺄셈이 모두 가능한 회로가 됩니다. 이것은 2의 보수법을 이용한 것입니다.
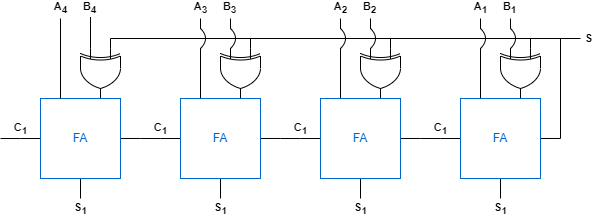
3. 캐리 예측 가산기(Carry Look-ahead Adder, CLA)
리플 캐리 가산기는 전가산기를 통해 간단하게 설계할 수 있지만, 비트수가 늘어날수록 연산속도가 느려진다는 문제가 있습니다. 왜냐하면 캐리를 입력으로 받기 때문에 상위 비트는 하위 비트가 계산될 때까지 연산을 하지 못하고 대기해야 하기 때문입니다. 이것을 해결하기 위해서 캐리 예측 가산기(CLA)를 사용할 수 있습니다.
캐리 예측 가산기는 부분 전가산기(Partial Full Adder, PFA)로부터 생성(Generation)과 전파(Propagation) 함수를 입력받아 이전 비트의 계산결과를 기다릴 필요 없이 연산을 한번에 할 수 있습니다.
부분 전가산기(PFA)는 전가산기(FA)에서 캐리 생성과 관련된 회로를 제외한 회로입니다. 캐리는 PFA에서 2개의 출력선에 의해 결정됩니다.
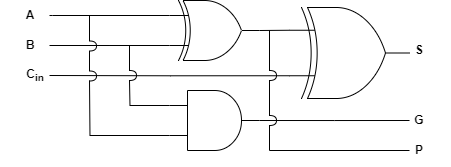
생성(G) 함수는 이전 비트의 결과값에 상관없이 캐리의 생성여부를 결정합니다. 부분 전가산기의 AND gate에 의해 출력된 값이 이에 해당합니다.
$ G(A, B) = A \cdot B $
전파(P) 함수는 이전 비트의 결과값에 따른 캐리의 생성여부를 출력합니다. 부분 전가산기의 XOR gate에 의해 출력된 값이 이에 해당합니다.
$ P(A, B) = A \oplus B $
G와 P를 통해 S와 C를 구하는 논리식을 다음과 같이 세울 수 있습니다.
$$ S_{i} = P_{i} \oplus C_{i} \\ C_{i+1} = G_{i} + P_{i} \cdot C_{i} $$
부분 전가산기 4개로 4비트 전가산기를 구성한다면 4개의 캐리에 대한 회로를 구성해야 합니다.
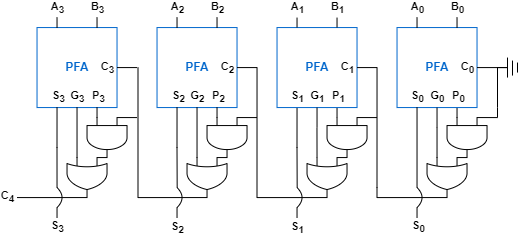
이렇게 구성된 4비트 가산기를 2개 연결하면 8비트 가산기, 4개 연결하면 16비트 가산기를 만들 수 있습니다.

디코더(Decoder) / 인코더(Encoder)
디코더는 입력 변수들의 최소항(minterm)을 생성하는 논리회로입니다. n개의 입력을 통해 2n개의 최소항을 출력합니다.
최소항은 진리표에서 하나의 행만 1이 되고 나머지는 0이 되는 곱을 말합니다. 예를 들어 2개의 입력을 통해 다음과 같이 4개의 최소항을 생성할 수 있습니다.
| A | B | D0 | D1 | D2 | D3 |
|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 |
해당 진리표를 통해 다음과 같이 회로를 그릴 수 있습니다.
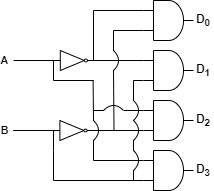
해당 회로를 활성화 또는 비활성화 시키기위해 다음과 같이 Enable 입력을 연결하면 2X4 디코더가 됩니다.
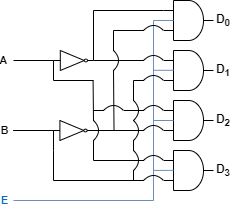
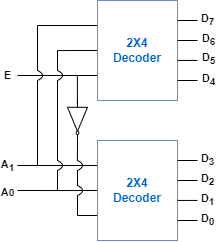
2X4 디코더를 2개 연결한다면 3X8 디코더를 만들 수 있습니다.
인코더는 디코더의 반대입니다. 2n개의 입력으로 부터 n개의 이진코드를 출력합니다.
| D0 | D1 | D2 | D3 | A | B |
|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 | 1 | 1 |
인코더는 OR gate를 통해 간단하게 회로를 구성할 수 있습니다.
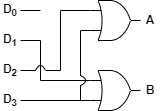
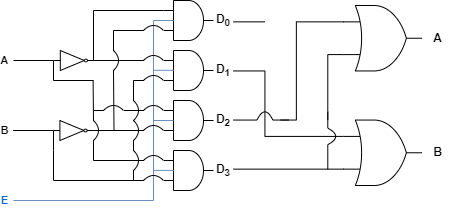
인코더를 통해 암호화된 출력이 디코더의 입력이 된다면 원래의 입력으로 해독할 수 있습니다.
멀티플렉서(Multiplexer, MUX)
멀티플렉서는 n개의 선택선 입력을 통해 2n개의 데이터 입력 중 하나를 선택하여 출력선으로 연결하는 논리회로입니다. 데이터 선택기(Data Selector)라고도 불립니다.
CPU에서 연산을 하기 위해서는 RAM으로부터 데이터를 가져와야합니다. 이때 데이터를 가져오는 가장 간단한 방법은 램과 레지스터를 1:1로 연결하는 것입니다.
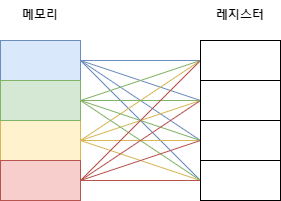
4비트만 연결해도 16개의 출력선이 필요하여 너무 복잡해집니다. 이를 해결하기 위해 멀티플렉서를 사용합니다. 멀티플렉서는 여러 입력 가운데서 하나의 입력을 선택하여 출력합니다.
n개의 제어 입력을 통해 2n개의 데이터 입력을 제어할 수 있습니다. 아래는 4비트의 입력선을 제어하기 위한 4X1 멀티플렉서 회로입니다.
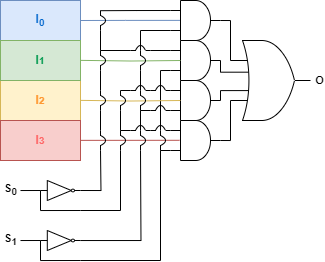
제어 입력선은 디코더와 동일하며, 디코더의 출력선은 데이터 입력선과 AND 연산을 통해 입력선을 선택할 수 있습니다.
멀티플렉서를 통해 메모리에서 출력된 데이터는 버스(bus)를 통해 CPU의 레지스터로 전달됩니다. 이때 2n개의 출력선 중 하나를 선택하여 전송하는데, 이것은 디멀티플렉서(Demultiplexer, DMUX)에 의해 수행됩니다.
디멀티플렉서의 회로 또한 n개의 제어 입력이 필요하며, 하나의 데이터 입력선과 AND 연산을 통해 출력선을 선택할 수 있습니다.
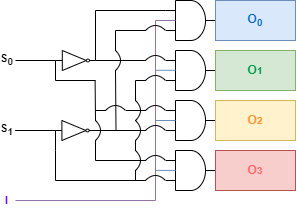
순차회로(Sequential Circuit)
순차회로는 출력값이 이전 상태와 현재 입력값에 영향을 받는 논리회로입니다. 즉, 조합회로에 기억 기능이 추가된 회로입니다.
순차회로는 클럭 신호에 의해 상태가 변하는 동기회로와 그렇지 않은 비동기회로로 나눌 수 있습니다.
순차회로가 1비트의 정보를 기억하는 방법은 피드백(Feedback) 경로라 불리는 폐루프를 형성하는 것입니다.
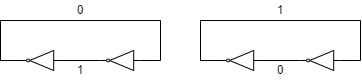
위의 회로와 같이 피드백을 통해 NOT 게이트 사이에 비트 정보를 저장할 수 있습니다.
래치(Latch)
래치는 클럭 입력을 가지지 않는 비동기회로입니다. 래치는 SR래치와 D래치가 있습니다.
1. S-R 래치
SR래치에서 S는 Set을 의미하며 1을 출력하고, R은 Reset을 의미하며 0을 출력합니다. 각각의 출력 Q와 Q’은 다시 입력으로 들어가서 피드백을 형성합니다.
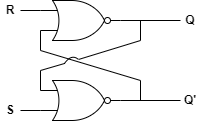
진리표는 다음과 같습니다.
| S | R | Q | $ \bar Q $ | 기능 |
|---|---|---|---|---|
| 0 | 0 | Q | $ \bar Q $ | 유지 |
| 0 | 1 | 0 | 1 | reset |
| 1 | 0 | 1 | 0 | set |
| 1 | 1 | 0 | 0 | 제한 |
$ R = 1, S = 0 $ 이면 $ Q = 0$ 이 출력되며, 출력된 Q는 S가 연결된 NOR 게이트로 피드백됩니다. $ S = 0 $ 이므로 $ \bar Q = 1 $ 이 출력되며, 출력된 $ \bar Q $ 는 R이 연결된 NOR 게이트로 피드백 됩니다. R이 연결된 NOR 게이트의 입력은 1, 1이 되므로 $ Q = 0 $ 이 되어 Reset 상태가 됩니다.
$ Q = 0, \bar Q = 1 $
반면 $ R = 0, S = 1 $ 이면 $ \bar Q = 0 $ 이 출력되며, 출력된 $ \bar Q $ 는 R이 연결된 NOR 게이트로 피드백됩니다. $ R = 0 $ 이므로 $ Q = 1 $ 이 출력되며, 출력된 Q는 S가 연결된 NOR 게이트로 피드백됩니다. NOR 게이트의 입력은 1, 1이 되므로 $ \bar Q = 0 $ 이 되어 Set 상태가 됩니다.
$ Q = 1, \bar Q = 0 $
$ R = 0, S = 0 $ 이면 $ Q = Q, \bar Q = \bar Q $ 가 되어 상태가 유지되며, $ R = 1, S = 1 $ 이면 Q와 $ \bar Q $ 가 0, 1 로 진동하게 되므로 입력이 제한됩니다.
NAND 게이트를 사용하여 SR 래치를 만들 수도 있습니다. 이 경우 입력이 반전됩니다.
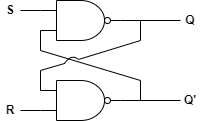
진리표는 다음과 같습니다.
| S | R | Q | $ \bar Q $ | 기능 |
|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 제한 |
| 0 | 1 | 1 | 0 | set |
| 1 | 0 | 0 | 1 | reset |
| 1 | 1 | Q | $ \bar Q $ | 유지 |
$ R = 0, S = 1 $ 이면 $ Q = 0, \bar Q = 1 $ 이 되어 reset 상태가 되며, $ R = 1, S = 0 $ 이면 $ Q = 1, \bar Q = 0 $ 이 되어 set 상태가 됩니다.
또한 $ R = 0, S = 0 $ 이면 Q와 $ \bar Q $ 가 0, 1 로 진동하므로 입력이 제한되며, $ R = 1, S = 1 $ 이면 $ Q = Q, \bar Q = \bar Q $ 가 되어 상태가 유지됩니다.
2. 게이트형 S-R 래치
게이트형 SR 래치는 Enable 이라 불리는 게이트 신호를 통해 출력을 결정하는 기억회로입니다.
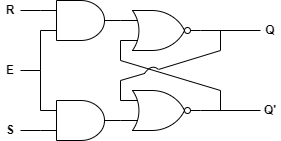
E 신호가 HIGH인 경우 래치의 입력이 출력에 반영되고, E 신호가 LOW인 경우 래치의 입력은 출력에 반영되지 않고 상태를 유지합니다.
3. D 래치
D 래치는 하나의 입력을 통해 출력 Q를 결정하는 회로입니다.
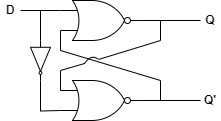
S = 0, R = 0 인 입력과 S = 1, R = 1 인 입력을 배제하여 입력과 출력이 동일한 회로를 만들 수 있습니다.
진리표는 다음과 같습니다.
| D | Q | $ \bar Q $ | 기능 |
|---|---|---|---|
| 0 | 0 | 1 | reset |
| 1 | 1 | 0 | set |
플립플롭(Flip-Flop)
플립플롭은 클럭 입력을 가지는 동기회로입니다.
엄밀하게 말하자면 래치 또한 클럭신호를 가질 수 있습니다. 하지만 CLOCK 신호가 HIGH인 동안 동작하는 래치와 달리 플립플롭의 경우 CLOCK 신호가 HIGH가 되는 순간에만 동작합니다.
래치의 경우
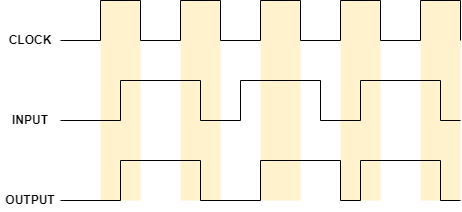
래치는 위와 같이 CLOCK이 HIGH이면 INPUT을 출력하고 CLOCK이 LOW이면 상태를 유지합니다.
플립플롭의 경우
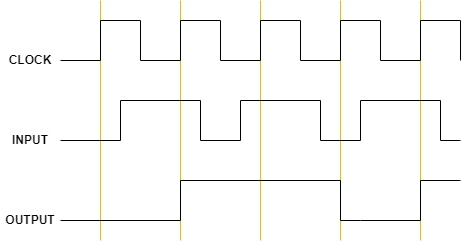
플립플롭의 경우 CLOCK이 HIGH가 되는 순간에만 INPUT을 출력하고 상태를 유지합니다.
1. S-R 플립플롭
S-R 플립플롭은 다음과 같이 게이트형 S-R 래치 2개로 구성할 수 있습니다.
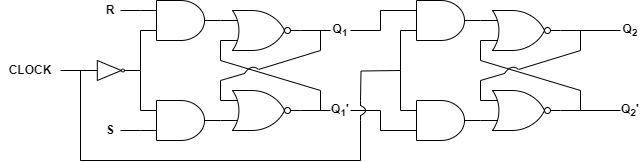
앞에 있는 래치를 마스터, 뒤에 있는 래치를 슬레이브라고 하기때문에 마스터-슬레이브 플립플롭이라고도 합니다.
아래 타이밍을 살펴보면 CLOCK이 HIGH인 순간에만 Q1의 상태가 Q2에 반영되고 2의 상태가 유지되는 것을 확인할 수 있습니다.
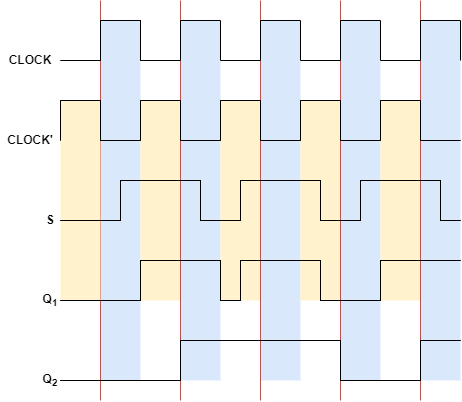
2. D 플립플롭
D 플립플롭은 다음과 같이 D 래치 2개로 구성할 수 있습니다.
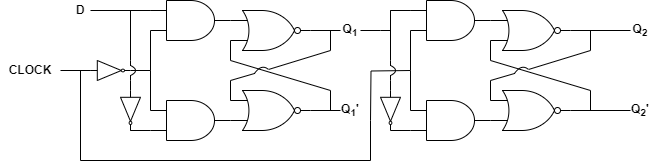
3. J-K 플립플롭
JK 플립플롭은 S = 1, R = 1 입력이 제한되는 문제를 보완하기 위한 회로입니다.
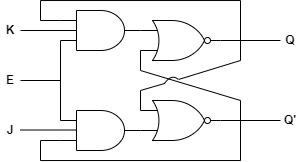
위와 같은 회로를 JK 래치라고 하며, J = 1, K = 1이 입력되면 $ Q = \bar Q $ 로 토글됩니다. 물론 하나의 JK 래치로는 반복적으로 토글되므로 2개의 JK 래치를 통해 플립플롭으로 구성한다면 CLOCK이 HIGH가 되는 순간에만 토글이 됩니다.
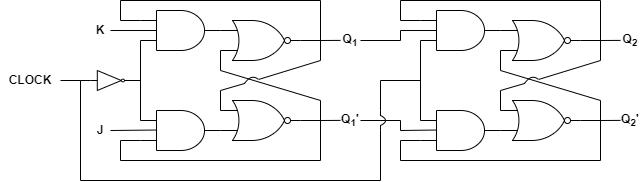
진리표는 다음과 같습니다.
| J | K | Q | $ \bar Q $ | 기능 |
|---|---|---|---|---|
| 0 | 0 | Q | $ \bar Q $ | 유지 |
| 0 | 1 | 0 | 1 | reset |
| 1 | 0 | 1 | 0 | set |
| 1 | 1 | $ \bar Q $ | Q | 토글 |
4. T 플립플롭
T 플립플롭은 JK 플립플롭에서 D 플립플롯처럼 입력을 하나만 주는 회로입니다. T가 0이면 이전값을 유지하고, T가 1이면 출력값이 토글 됩니다.
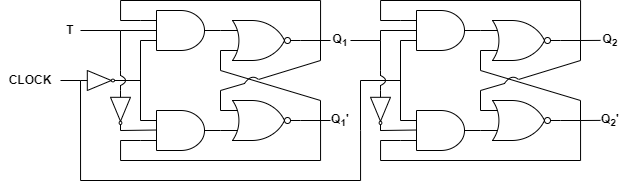
진리표는 다음과 같습니다.
| T | Q1 | Q2 | 기능 |
|---|---|---|---|
| 0 | 0 | 0 | 유지 |
| 0 | 1 | 1 | 유지 |
| 1 | 0 | 1 | 토글 |
| 1 | 1 | 0 | 토글 |