조합과 순열
조합과 순열은 알고리즘 문제를 풀다보면 자주 만나는 문제 유형 입니다. 백트래킹, 분할정복 등 많은 알고리즘에 조합과 순열이 포함됩니다.
조합은 서로 다른 n개의 원소를 가지는 집합에서 r개의 원소를 순서에 상관없이 선택하는 것을 의미하며, 순열은 서로 다른 n개의 원소를 가지는 집합에서 r개의 원소를 순서대로 선택하는 것을 의미합니다.
이번 글에서는 조합과 순열에 대해 자세히 알아보고, 예제를 통해 코드를 작성해보도록 하겠습니다.
팩토리얼(Factorial)
서로 다른 n개를 나열하는 경우의 수를 팩토리얼이라고 하며. 기호로는 !로 나타냅니다.
$$ n! = n(n-1)(n-2) \cdots 1 $$
자바스크립트 코드
function factorial(n) {
return n > 1 ? n * factorial(n-1) : 1;
}
조합(Combination)
서로 다른 n개의 원소를 가지는 어떤 집합에서 r개의 원소를 순서에 상관없이 선택하는 것을 조합이라고 하며, 기호로는 $ _{n}\mathrm{C}_{r} $로 나타냅니다.
$$ _{n}\mathrm{C}_{r} = {n! \over (n-r)!n!} $$
중복조합
중복 가능한 n개의 원소 중 r개의 원소를 순서에 상관없이 선택하는 것을 조합이라고 하며, 기호로는 $ _{n}\mathrm{H}_{r} $로 나타냅니다.
$$ _{n}\mathrm{H}_{r} = _{n+r-1}\mathrm{C}_{r} $$
문제
음이 아닌 정수 xx, yy, zz에 대해, $ x+y+z \le 3 $를 만족시키는 순서쌍 (x,y,z)의 수는?
풀이
주어진 식은 $ x + y + z = 3 - n (0 \le n \le 3) $ 으로 나타낼 수 있으며, 정수 x, y, z, n 에 대하여 $ x+y+z+n=3 $을 만족해야 합니다.
즉, 0 ~ 3 중 3개를 순서에 상관 없이 선택하는 중복조합에 해당합니다.
그러므로 $ _4\mathrm{H}_3 = _6\mathrm{C}_3 = {6! \over 3!3!} = 20$ 이 됩니다.
순열(Permutation)
서로 다른 n개의 원소를 가지는 어떤 집합에서 r개의 원소를 순서대로 선택하는 것을 순열이라고 하며, 기호로는 $ _{n}\mathrm{P}_{r} $로 나타냅니다.
$$ _{n}\mathrm{P}_{r} = {n! \over (n-r)!} $$
중복순열
중복 가능한 n개의 원소 중 r개의 원소를 순서대로 선택하는 것을 중복순열이라고 하며, 기호로는 $ _{n}\mathrm{\Pi}_{r} $로 나타냅니다.
$$ _{n}\mathrm{\Pi}_{r} = n^r $$
소스 코드
조합과 순열은 백트래킹을 통해 구현할 수 있습니다.
swap을 통한 백트래킹
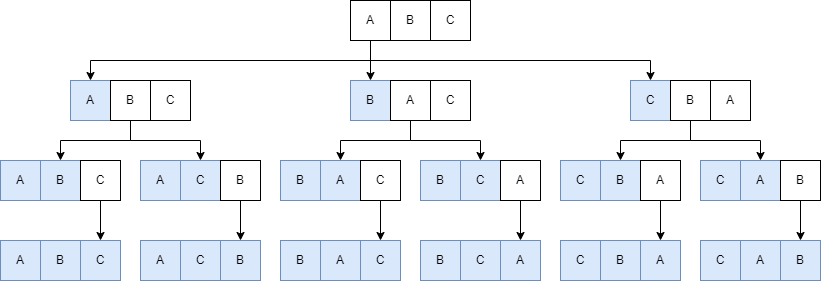
배열의 첫번째 값을 순차적으로 바꿔 전체적으로 한번씩 swap 된 형태로 순열을 출력합니다. depth를 기준으로 인덱스가 depth보다 작으면 고정시키고, depth보다 크면 다시 swap을 진행합니다.
자바스크립트 코드
function permutation(arr, n = arr.length, r = n, depth = 0, output = []) {
if(depth === r) {
output.push(arr.slice());
return;
}
for(let i = depth; i < n; i++) {
swap(arr, depth, i);
permutation(arr, n, r, depth + 1, output);
swap(arr, depth, i);
}
if (depth === 0) return output;
function swap(arr, depth, i) {
const temp = arr[depth];
arr[depth] = arr[i];
arr[i] = temp;
}
}
console.log(permutation(["A", "B", "C"]));
// ------- 출력 --------
// 0: (3) ['A', 'B', 'C']
// 1: (3) ['A', 'C', 'B']
// 2: (3) ['B', 'A', 'C']
// 3: (3) ['B', 'C', 'A']
// 4: (3) ['C', 'B', 'A']
// 5: (3) ['C', 'A', 'B']
swap을 한 후 함수를 depth가 r이 될때까지 재귀호출을 합니다. 값이 돌아오면 다시 swap을 하여 배열을 원래상태로 되돌립니다.
이 방법은 별도의 공간을 필요로 하지 않기 때문에 공간복잡도는 작지만 순열의 순서를 보장하지는 않습니다. 위에 출력된 코드를 보면 4번째 출력은 C -> A -> B 가 출력되어야 하지만, C -> B -> A 가 먼저 출력됨을 볼 수 있습니다.
visited 배열을 통한 백트래킹
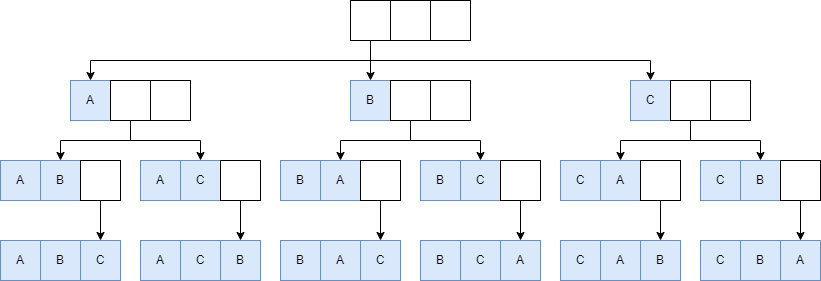
이 방법은 깊이우선탐색(DFS)를 통해 모든 인덱스를 방문합니다. 이때 visited 배열을 통해 중복값이 다시 들어가지 않도록 하면서 output 배열을 채워나갑니다.
자바스크립트 코드
function permutation(arr, n = arr.length, r = n, depth = 0, visited = [], output = [], result = []) {
if(depth === r) {
result.push(output.slice());
return;
}
for(let i = 0; i < n; i++) {
if(!visited[i]) {
visited[i] = true;
output[depth] = arr[i];
permutation(arr, n, r, depth + 1, visited, output, result);
visited[i] = false;
}
}
if (depth === 0) return result;
}
console.log(permutation(["A", "B", "C"]));
// ------- 출력 --------
// 0: (3) ['A', 'B', 'C']
// 1: (3) ['A', 'C', 'B']
// 2: (3) ['B', 'A', 'C']
// 3: (3) ['B', 'C', 'A']
// 4: (3) ['C', 'A', 'B']
// 5: (3) ['C', 'B', 'A']
추가적인 공간을 필요로 하기에 공간 복잡도가 증가하지만 순열의 순서를 보장합니다.
비트셋을 통한 조합
아이템의 존재 유무는 1 또는 0으로 표현할 수 있으므로, n개의 비트를 통해 n개의 아이템에 대한 하나의 상태를 표현할 수 있습니다.
자바스크립트 코드
const items = ["A", "B", "C"];
위에 작성한 아이템 배열의 경우, A = 1 « 0, B = 1 « 1, C = 1 « 2 로 나타낼 수 있습니다. 이는 각각 $ 2^0, 2^1, 2^2 $을 나타냅니다. 즉, $ 2^n $까지 순회하여 비트셋을 해석하면 r에 대한 모든 조합을 얻을 수 있습니다.
function combination(arr, r = 0) {
const output = [];
const length = arr.length;
for(let i = 0; i < 2**length; i++) {
const cur = [];
for (let j = 0; j < length; j++) {
if (i & (1 << j)) cur.push(arr[j]);
}
if(!r || cur.length === r) output.push(cur);
}
return output;
}
관련 문제
- 프로그래머스(Programmers)