최대공약수와 최소공배수
최대공약수와 최소공배수
최대공약수(GCD, Greateast Common Division)는 두 수에 대한 공약수의 최대값을 의미하며, 최소공배수(LCM, Least Common Multiple)는 두 수에 대한 공배수의 최소값을 의미합니다.
최대공약수와 최소공배수는 소인수분해(Integer factorization)를 통해 구할 수 있습니다.
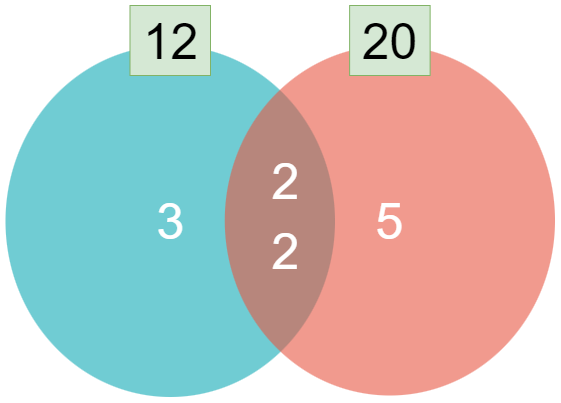
최대공약수는 소인수의 교집합을 모두 곱한 값이고, 최소공배수는 소인수의 합집합을 모두 곱한 값입니다. 예를 들어 a = 12, b = 20 인 경우, a와 b의 최대공약수와 최소공배수는 다음과 같이 구할 수 있습니다.
a = 12 =
2 * 2* 3
b = 20 =2 * 2* 5
a와 b의 소인수에 대한 교집합은 [2, 2]가 되고, 이를 모두 곱한 4가 최대공약수가 됩니다. 또한 a와 b의 소인수에 대한 합집합은 [2, 2, 3, 5]가 되고, 이를 모두 곱한 60이 최소공배수가 됩니다.
최대공약수를 G, 최소공배수를 L이라고 한다면, 다음과 같은 식이 성립합니다.
a = 12 = G * A
b = 20 = G * BA = a/G B = b/G
L = G * A * B = G * (a/G) * (b/G) = a*b/G
이때 A와 B는 서로소가 됩니다.
이를 자바스크립트 코드로 나타내면 다음과 같습니다.
function GCD(a, b) {
let result = 1;
if(a > b) [a, b] = [b, a];
let i = 2;
while(1) {
while(a%i === 0 && b%i === 0) {
a /= i;
b /= i;
result *= i;
}
if(a === 1 || a === i++) return result;
}
}
function LCM(a, b) {
return a * b / GCD(a, b);
}
유클리드 호제법(Euclidean algorithm)
두 양의 정수 a, b (a > b)에 대하여 a = bq + r (0 ≤ r < b)이라 하면, a, b의 최대공약수는 b, r의 최대공약수와 같다.
즉,
gcd(a, b) = gcd(b, r)이다.r = 0이라면, a, b의 최대공약수는 b가 된다.
유클리드 호제법(Euclidean algorithm)은 두 양의 정수, 혹은 두 다항식의 최대공약수를 구하는 방법입니다. 이 알고리즘은 유클리드의 원론에 적혀있는 내용으로, 인류 최초의 알고리즘이라 합니다.
소인수 분해를 통해 최대공약수를 구하면 시간 복잡도가 O(N) 이지만, 유클리드 호제법으로 최대공약수를 구하면 시간 복잡도를 O(logN)으로 줄일 수 있습니다.
증명
gcd(a, b) = G, gcd(b, r) = G' 라고 가정 한다면, 서로소인 두 정수 A, B에 대하여 a = GA, b = GB가 성립합니다.
이를 a = bq + r에 대입하면, GA = GBq + r 이므로 r = G(A - Bq)가 됩니다. 여기서 G는 b와 r의 공약수임을 확인할 수 있으며, 그러므로 G는 G'의 약수임을 알 수 있습니다.
G' = mG라고 가정한다면, 서로소인 두 정수 k, l에 대하여 b = GB = G'k = Gmk, r = G(A - Bq) = G'l = Gml이 성립하며, 양변을 G로 나누면 B = mk, A - Bq = ml이 됩니다.
두 연립 방정식에 의하여 A = ml + Bq = ml + mkq = m(l + kq) 가 되므로, m은 A와 B의 공약수가 됨을 알 수 있습니다.
여기에서 A와 B는 서로소 관계에 있으므로, m = 1 이 되며, G' = mG라고 가정했으므로 G' = G 가 됩니다.
즉, gcd(a, b) = gcd(b, r)입니다.
r = 0인 경우 a = bq 이므로, b가 최대공약수가 됩니다.
소스 코드
자바스크립트 코드
function GCD(a, b) {
return b ? GCD(b, a % b) : a;
}
function LCM(a, b) {
return a * b / GCD(a, b);
}
자바 코드
public Euclidean {
public static int GCD(int a, int b) {
return b == 0 ? a : GCD(b, a%b);
}
public static int LCM(int a, int b) {
return a * b / GCD(a, b);
}
}
파이썬 코드
def GCD(a, b):
return a if b == 0 else GCD(b, a%b)
def LCM(a, b):
return a * b / GCD(a, b)
C 코드
int GCD(int a, int b) {
return b ? GCD(b, a%b) : a;
}
int LCM(int a, int b):
return a * b / GCD(a, b);
관련 문제
- 프로그래머스(Programmers)